Tutorial Decibel: dB și dBm vs. Gain și Milliwatts

Conceptul de decibel (dB) este înțeles dificil și confuz pentru cineva care tocmai i se introduce. Combinarea specificațiilor pentru câștig, putere și tensiune (și curent, dar nu atât de des) care amestecă dB, dBm, dBW, wați, miliwati, tensiune, milivolți etc., necesită adesea conversia înainte și înapoi între valori liniare și valori decibelice. Acest scurt tutorial va ajuta la clarificarea diferenței dintre a lucra cu decibeli și a lucra cu valori liniare.

Logaritmele (jurnalele) au fost concepute pentru prima dată în 1600-urile timpurii de matematicianul scotian John Napier, ca un instrument de simplificare a operațiilor de înmulțire și divizare, transformându-le în operații de adunare și scădere predispuse la erori mai rapide și mai puțin. Acest lucru este posibil datorită modului în care multiplicarea a două numere exprimate ca numere de bază similare cu exponenți poate fi realizată doar prin adăugarea exponenților împreună. Împărțirea acelorași numere se realizează scăzând exponenții. Este una dintre legile exponenților și arată astfel:

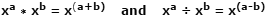
Folosind numere reale ca exemplu, unde x = 10, a = 4, b = 1:

Legea exponenților funcționează pentru orice număr de bază, nu doar pentru 10. A ingenui:

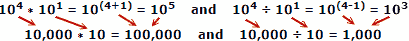
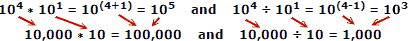
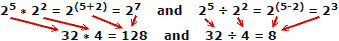
Oamenii tind să facă mai puține greșeli atunci când adaugă și scad numere, astfel încât avantajul logaritmelor este evident. Nu uitați că logaritmele au fost dezvoltate înainte ca computerele mecanice sau electronice automate să fie disponibile. O regulă de diapozitive exploatează proprietățile logaritmelor pentru calcul, dar acesta este un subiect major separat.

Acestea sunt exemple simple, dar păstrează orice bază sau exponent. În absența unui calculator, pentru a putea fi util pentru o aplicație generală, aveți nevoie de un tabel cu numere și logaritmele lor echivalente. Tabelele de jurnal timpuriu au umplut volume, în funcție de distanța dintre numere (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3 etc.). Vestea bună pentru creatorii de tabele de logaritm este că doar o singură „decadă” de numere (de exemplu, 1 prin 10) este necesară, deoarece fiecare deceniu precedent sau în secțiune este un simplu simplu al unei puteri de 10.

Notă: Folosesc baza 10 în această discuție, deoarece aceasta este baza sistemului nostru de numere comun - de unde și termenul „logaritm comun” pentru jurnalele de bază 10. Este posibil să fi auzit de logaritmi naturali, care utilizează baza lui e, dar e nu este utilizat foarte des atunci când se calculează puterea electrică scalară, tensiunea și cantitățile actuale (deși este utilizat atunci când sunt incluse unghiurile de fază, adică identitatea lui Euler). Logaritmele naturale sunt scrise ca ln (x) fără subscripția „e”, în timp ce logaritmele 10 de bază sunt scrise pur și simplu sub formă de log (x) fără subscriptul 10; adică, nu loge (x) sau log10 (x), respectiv.

Pe o bază = tabelul de jurnal 10:

Hârtie grafică 5 Cycles Semi-Logaritmice pentru inginerie - RF CafeCazul excepțional și special este logx (0) = nedefinit. Acest lucru se întâmplă pentru că nu există nicio putere la care să puteți ridica orice număr și să obțineți 0 (zero). Puteți aborda asimptotic zero, dar nu puteți ajunge la zero. Nu va fi niciodată numărul zero afișat pe o scară de jurnal; de obicei, acestea merg de la o putere 10 la o altă putere de zece. Un exemplu de hârtie cu grafic de jurnal este afișat în partea dreaptă. Are 5 „cicluri” sau „zeci de ani”. Rețineți că nu există zero pe axa y.

Logaritmul de bază 10 (comun) al unui număr este apoi exponentul la care trebuie ridicat 10 pentru a obține acest număr. Cu alte cuvinte, deoarece 10 crescut la puterea lui 2 este egal cu 100 (102 = 100), jurnalul de bază 10 al 100 este 2 (log10 100 = 2).

Aceasta este legea de bază a logaritmelor:


Efectuarea acelorași înmulțiri și diviziuni ca în partea de sus a paginii utilizând logaritmele reale:



E în regulă, dar cu ceea ce termini este logaritmul numărului pe care îl cauți. Întrebare: Cu excepția unui exemplu simplu ca acesta, cum obțineți răspunsul de care aveți nevoie? Răspuns: Căutați antilogaritmul (antilogul) rezultatului. În acest caz:

Un exemplu mai dur și, mai probabil, cu numere care nu sunt puteri întregi de 10, ar putea arăta ca acesta:




 Calculatorul HP-35 (wikipedia) - RF Cafe Din momentul în care logaritmul „x” este egal cu 1.8444, antilogul este egal cu „x”, care este 69.9



Am folosit calculatorul meu pentru a căuta jurnalele și antilogurile pentru aceste numere, dar înainte de 1972 când Hewlett Packard (HP) a introdus calculatorul științific HP-35, persoana obișnuită fără acces la un computer mainframe corporativ sau universitar necesar pentru a utiliza un jurnal tabel pentru a efectua astfel de calcule.

Cine se deranjează să folosească logaritmele astăzi, s-ar putea să întrebi? O mulțime de oameni, inclusiv eu, destul de des atunci când se calculează parametrii sistemului în cascadă, cum ar fi cifra de zgomot (NF) și punctele de interceptare (IP). Adăugarea și scăderea simplă a valorilor dB de câștig și puterea dBm nu funcționează cu NF și IP. Formulele de guvernare utilizează multiplicarea și divizarea valorilor câștigului și puterii liniare, ceea ce necesită mai întâi conversia dB și / sau dBm în numere liniare (raportul de câștig și mW) folosind antiloguri, efectuând calculele în cascadă, apoi convertind rezultatul înapoi la dB și / sau dBm folosind jurnalele.

Nu toate operațiile în cascadă ale sistemului necesită conversie înainte și înapoi. De exemplu, dacă este nevoie doar de câștigul total și / sau nivelul de putere de ieșire, atunci calculele pot fi efectuate fie cu unități liniare (mW și multiplicatori), fie cu unități logaritmice (dBm și, respectiv, dB).

Definiția „dB” și „dBm”

Un decibel (dB) în inginerie electrică este definit ca 10 de ori logaritmul 10 de bază al unui raport între două niveluri de putere; de exemplu, Pout / Pin (câștig, cu alte cuvinte). A ingenui:

Prin urmare, toate câștigurile mai mari de 1 sunt exprimate ca decibeli pozitivi (> 0), iar câștigurile mai mici de 1 sunt exprimate ca decibeli negativi (<0). Rețineți că, pentru cazurile în care majoritatea dintre noi întâlnim, raportul liniar P1 / P2 trebuie să fie un număr pozitiv (> 0), deoarece logaritmul lui 0 este nedefinit, iar logaritmul numerelor negative sunt complexe (ele conțin atât o parte reală, cât și o parte imaginară ). Valoarea dB, totuși, poate prelua teoretic orice valoare între −∞ și + ∞, inclusiv 0, care este un câștig de 1 [10 * log (1) = 0 dB].

„dBm” este o unitate de putere bazată pe decibeli, la care se face referire la 1 mW. Deoarece 0 dB de câștig este egal cu un câștig de 1, 1 mW de putere este 0 dB mai mare decât 1 mW sau 0 dBm. În mod similar, o unitate de putere de dBW este decibeli în raport cu puterea 1 W.


În consecință, toate valorile dBm mai mari decât 0 sunt mai mari decât 1 mW și toate valorile dBm mai mici decât 0 sunt mai mici decât 1 mW (a se vedea Fig. 1). De exemplu, + 3.01 dBm este 3.01 dB mai mare decât 1 mW; adică, sau 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). −3.01 dBm este 3.01 dB mai mic decât 1 mW; adică sau 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).

Următorul tabel oferă câteva exemple numerice, astfel încât să puteți vedea corelația dintre mW și dBm. Același set de valori reprezentat pe o scară logaritmică ar produce o linie dreaptă. Din cauza relației logaritmice, graficul grupează valorile mai mici față de axa verticală stângă. O versiune mărită a regiunii 0 până la 1 mW este introdusă pentru claritate.

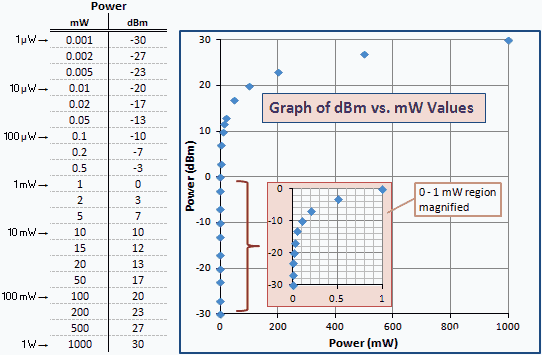
Fig. 1 - Graficul puterii în unități de dBm vs. mW

Fig. 2 este un tabel și un grafic al raporturilor de câștig dB vs. lineare similare cu dBm față de mW în Fig. 1. Rețineți că numerele și curbele sunt exact aceleași; numai etichetele axelor sunt schimbate. Acest lucru se datorează faptului că dBm este o unitate de putere exprimată în dB în raport cu 1 mW (0 dBm).

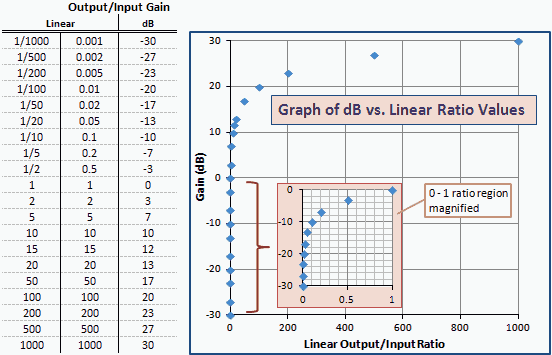
Fig. 2 - Graficul câștigului în unități de dBm față de raportul liniar

Fundamental, câștigul este un factor de înmulțire (sau divizare). Ca exemplu, un amplificator poate avea un câștig care mărește semnalul cu un factor de 4 (adică 4x) de la intrare la ieșire (a se vedea Fig. 3). Dacă un semnal 1 mW (0 dBm) este introdus în amplificator, atunci 1 mW * 4 = 4 mW apare. În ceea ce privește decibelii, un factor de 4 este echivalent cu 10 * log (4) = 6.02 dB, deci 0 dBm în plus 6.02 dB de randament câștig + 6.02 dBm la ieșire.

1 mW * 4 = 4 mW

0 dBm + 6.02 dB = 6.02 dBm

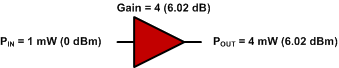
Fig. 3 - Câștig amplificator unic.

Combinarea câștigurilor (liniară și dB) cu valoarea pozitivă

Dacă un amplificator cu un câștig de 4 este în serie cu un al doilea amplificator cu un câștig de 6, atunci câștigul total este 4 * 6 = 24. În ceea ce privește decibelii, un factor de 6 este echivalent cu 10 * log (6) = 7.78 dB, iar un factor de 24 este echivalent cu 10 * log (24) = 13.8 dB.

La fel ca 4 x 6 = 24 (câștig liniar), 6.02 dB + 7.78 dB = 13.8 dB (câștig decibel).

Dacă un semnal 1 mW (0 dBm) este introdus în amplificator, atunci 4 mW iese din primul amplificator, iar 24 mW iese din al doilea amplificator. Vezi fig. 4.

1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Fig. 4 - Câștig amplificator dublu în cascadă.

Combinarea câștigului și pierderii (liniar și dB)
Următorul exemplu arată ce se întâmplă atunci când se întâlnește un câștig <1 (o pierdere), unde un atenuator cu un câștig de 1/6 este plasat după primul amplificator în loc să aibă un al doilea amplificator. Vezi Fig. 5.
4 * 1 / 6 = 2 / 3 (câștig liniar). În mod similar 6.02 dB - 7.78 dB = −1.76 dB (câștig decibel).
Ca și în exemplul precedent, dacă un semnal 1 mW (0 dBm) este introdus în amplificator cu un câștig de 4, atunci 4 mW iese. Acest 4 mW trece apoi în atenuator cu un câștig liniar de 1 / 6 și iese la un nivel de putere de 4 / 6 mW (2 / 3 mW).
Câștigul total în acest caz este 4 / 6 = 2 / 3, deci puterea de ieșire va fi de fapt mai mică decât puterea de intrare.

1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW

0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

Fig. 5 - Câștig amplificator și atenuator în cascadă.

12 mW + 34 mW + 8 mW + 20 dB

Informații suplimentare despre logaritmi
Logaritmele produselor
O proprietate a logaritmelor utilizate implicit mai sus menționează următoarele și este baza pentru a putea adăuga și scădea valorile logaritmului în loc să-și multiplice echivalentele liniare.

„h * j / k * m / n” poate reprezenta o cascadă de componente care au trei dispozitive (h, j și m) fiecare cu câștig> 1 și două dispozitive (k și n) fiecare cu un câștig <1 (a se vedea Fig. 6). Câștigul total al sistemului poate fi calculat fie prin înmulțirea tuturor valorilor de câștig liniar împreună, fie prin adăugarea tuturor valorilor de câștig decibel împreună.

Fig. 6 - Componente în cascadă

Logaritmele exponenților
Următorul lucru este important pentru a înțelege de ce câștigul de energie în termeni de putere este 10 * log (Pout / Pin) dB, în timp ce câștigul de energie din punct de vedere al tensiunii este 20 * log (Vout / Vin) dB.


ceea ce se întâmplă pentru că cf este egal cu c înmulțit de el însuși „f” ori. De exemplu, dacă f = 4:


Câștig de putere bazat pe putere vs. câștig de putere bazat pe tensiune
Câștigul de putere este Pout / Pin, iar câștigul de tensiune este Vout / Vin. Câștigul de putere bazat pe un raport de putere în decibeli este definit ca 10 * log (Pout / Pin). Câștigul de putere din punct de vedere al tensiunii este [(Vout2 / R) / (Vin2 / R)], deoarece legea lui Ohm P = V2 / R. „R” în numitori anulează ieșirea din Vout2 / Vin2, care este egală cu (Vout / Vin) 2, așa cum este definită de regula exponenților care spune ac / bc = (a / b) c. De aici:

Important Nota: Câștigul de tensiune din punct de vedere al tensiunii este 10 * log (Vout / Vin) dB, la fel ca în cazul câștigului de energie din punct de vedere al puterii. Ecuația 20 * log (Vout / Vin) dB se aplică numai când câștigul de putere este exprimat în termeni. Acesta este un punct comun de confuzie.


Nicio operațiune în matematică nu este arbitrară și acest lucru este valabil pentru motivul pentru care o pierdere de putere a semnalului (câștig <1) este prezentată ca o valoare negativă și, prin urmare, este scăzută în timpul unui calcul în cascadă. Este o demonstrație simplă, dar demnă de menționat.

log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)

Dacă doriți să construiți un post de radio, creșteți emițătorul de radio FM sau aveți nevoie de altul Echipamente FM, vă rugăm să nu ezitați să ne contactați: [e-mail protejat].

Lăsaţi un mesaj 

Lista de mesaje